ofic虚拟货币

2023年06月16日 14:43

欧易okx交易所下载

欧易交易所又称欧易OKX，是世界领先的数字资产交易所，主要面向全球用户提供比特币、莱特币、以太币等数字资产的现货和衍生品交易服务，通过使用区块链技术为全球交易者提供高级金融服务。

我们知道，优矿有400+因子库。随着因子库的不断增加，因子库内部有很多因子的信息是会有重复的，或者新检验的有效的因子与因子库里的因子也存在一定的相关性。并且因子也不是越多就越好。本文先研究东方的Alpha因子库精简与优化——《因子选股系列研究之十》是怎么做的。东方证券：Alpha因子库精简与优化——《因子选股系列研究之十》

import numpy as npimport pandas as pdfrom datetime import datetime, timedeltaimport timeimport matplotlib.pyplot as pltfrom sklearn.linear_model import LinearRegression import statsmodels.api as smimport scipy.stats as stimport seaborn as snssns.set_style('white')from CAL.PyCAL import *    # CAL.PyCAL中包含fontuniverse = set_universe('A')

1 定价因子检验

1.1 GRS 检验

这部分可以直接参考GRS检验，本文不再进行说明。

1.2 Fama-MacBeth检验

先来看什么是Fama-MacBeth回归：The Fama-MacBeth regression is a method used to estimate parameters for asset pricing models such as the Capital asset pricing model (CAPM). The method estimates the betas and risk premia for any risk factors that are expected to determine asset prices. The method works with multiple assets across time (panel data). The parameters are estimated in two steps:

First regress each asset against the proposed risk factors to determine that asset’s beta for that risk factor.
Then regress all asset returns for a fixed time period against the estimated betas to determine the risk premium for each factor.

再来看东方的说明：Fama-MacBeth检验该检验方法由Fama & MacBeth (1973)年提出，它是一种截面回归检验方法。如果从风险溢价出发，Fama-MacBeth回归是一个两步过程：Step 1. 对每个资产做时间序列回归，计算各个资产的因子暴露估计量bi,k；Step 2. 在每个横截面上用当期的资产收益率对期初的因子暴露估计量做横截面回归，得到风险溢价的估计λk,t对因子k，对序列{λk,t,t=1,2,…,T}做传统student-t检验，如果该因子有效，序列的均值应该显著不等于零。如果是从风险暴露出发，则可免去第一步，直接从第二步开始。本文即从风险暴露出发。

2 备选的因子

我这里选择了优矿400+因子库里面的若干个因子：

BP，市净率倒数
OperatingRevenueGrowRate，营业收入增长率
NetProfitGrowRate，净利润增长率
RETURNS_1m， 1个月反转收益因子
RETURNS_3m，3个月反转收益因子
ILLIQUIDITY，非流动性因子
VOL20，20日平均换手率因子
IVR，特异度因子

def getUqerStockFactors(begin, end, universe, factor):    """    使用优矿的因子DataAPI，拿取所需的因子，并整理成相应格式，返回的因子数据    格式为pandas MultiIndex Series，例如：    secID        tradeDate     002130.XSHE  2016-12-20    0.0640                 2016-12-21    0.0643                 2016-12-22    0.0631                 2016-12-23    0.0641                 2016-12-26    0.0667    注意：后面拿取因子的DataAPI可以自行切换为专业版API，以获取更多因子支持                     Parameters    ----------    begin : str        开始日期，'YYYY-mm-dd' 或 'YYYYmmdd'    end : str        截止日期，'YYYY-mm-dd' 或 'YYYYmmdd'    universe: list        股票池，格式为uqer股票代码secID    factor: str        因子名称，uqer的DataAPI.MktStockFactorsOneDayGet(或        专业版对应API)可查询的因子            Returns    -------    df : pd.Series - MultiIndex        因子数据，index为tradeDate、secID.    """        # 拿取上海证券交易所日历    cal_dates = DataAPI.TradeCalGet(exchangeCD=u"XSHG", beginDate=begin, endDate=end)    cal_dates = cal_dates[cal_dates['isOpen']==1].sort('calendarDate')    # 月工作日列表    cal_dates = cal_dates['calendarDate'].values.tolist()    month_list = [cal_dates[0]]    for i in range(len(cal_dates)-1):        if cal_dates[i][0:7] != cal_dates[i+1][0:7]:            month_list.append(cal_dates[i+1])    cal_dates = month_list        print  factor + ' will be calculated for ' + str(len(cal_dates)) + ' months:'    count = 0    secs_time = 0    start_time = time.time()        # 按天拿取因子数据，并保存为一个dataframe    df = pd.DataFrame()    for dt in cal_dates:        # 拿取数据dataapi，必要时可以使用专业版api        dt_df = DataAPI.MktStockFactorsOneDayProGet(tradeDate=dt, secID='',                                                  field=['tradeDate', 'secID']+[factor])        if df.empty:            df = dt_df        else:            df = df.append(dt_df)                # 打印进度部分，每200天打印一次        if count > 0 and count % 200 == 0:            finish_time = time.time()            print count,            print '  ' + str(np.round((finish_time-start_time) - secs_time, 0)) + ' seconds elapsed.'            secs_time = (finish_time-start_time)        count += 1            # 提取所需的universe对应的因子数据    df = df.set_index(['tradeDate','secID'])[factor].unstack()    universe = list(set(universe) & set(df.columns))    df = df[universe]    df.index = pd.to_datetime(df.index, format='%Y-%m-%d')        # 将上市不满三个月的股票的因子设置为NaN    equ_info = DataAPI.EquGet(equTypeCD=u"A",secID=u"",ticker=u"",listStatusCD=u"",field=u"",pandas="1")    equ_info = equ_info[['secID', 'listDate', 'delistDate']].set_index('secID')    equ_info['delistDate'] = [x if type(x)==str else end for x in equ_info['delistDate']]    equ_info['listDate'] = pd.to_datetime(equ_info['listDate'], format='%Y-%m-%d')    equ_info['delistDate'] = pd.to_datetime(equ_info['delistDate'], format='%Y-%m-%d')    equ_info['listDate'] = [x + timedelta(90) for x in equ_info['listDate']]    for sec in df.columns:        sec_info = equ_info.ix[sec]        df.loc[:sec_info['listDate'], sec] = np.NaN        df.loc[sec_info['delistDate']:, sec] = np.NaN        # 注意这里的shift，如此转换后，对于特定交易日的因子数据，对应的就是该交易日    # 可见的数据：2016-12-27这日的因子数据，只能由2016-12-26这天和这天之前的相    # 关数据计算得到    # df = df.shift(1).stack()    return df

def getUqerPrices(begin, end, universe, price='openPrice'):    """    使用优矿的行情DataAPI，拿取所需的行情数据，并整理成相应格式，返回的数据    格式为pandas DataFrame，例如：        secID       002233.XSHE  600687.XSHG  002596.XSHE ...    tradeDate                                                                         2016-01-04       14.355       23.357       42.951    2016-01-05       12.062       19.744       35.400    2016-01-06       12.209       21.361       36.139    2016-01-07       12.601       21.341       34.660    2016-01-08       11.915       19.964       32.363        Parameters    ----------    begin : str        开始日期，'YYYY-mm-dd' 或 'YYYYmmdd'    end : str        截止日期，'YYYY-mm-dd' 或 'YYYYmmdd'    universe: list        股票池，格式为uqer股票代码secID    factor: str        行情对应名称，uqer的行情api可以获取的行情名称            Returns    -------    df : pd.DataFrame        行情数据，index为tradeDate，columns为secID.    """        # 拿取上海证券交易所日历，并将拟拿取数据交易日分段    step = 200  # 每段长度    trade_cal = DataAPI.TradeCalGet(exchangeCD=u"XSHG", beginDate=begin, endDate=end)    trade_cal = trade_cal[trade_cal['isOpen']==1].sort('calendarDate')    cal_tmp = trade_cal.ix[::step]    # dates_tup 保存分段之后的每段的起止日期，备用    dates_tup = zip(cal_tmp.calendarDate, cal_tmp.prevTradeDate.shift(-1).dropna().tolist() + [end])                               print  price + ' will be read in ' + str(len(dates_tup)) + ' pieces:'    count = 0    secs_time = 0    start_time = time.time()        # 分段读取数据，并进行拼接    df = pd.DataFrame()    for x,y in dates_tup:        dt_df = DataAPI.MktEqudAdjGet(beginDate=x, endDate=y, secID=universe,                                       field=['tradeDate', 'secID']+[price])        if df.empty:            df = dt_df        else:            df = df.append(dt_df)                # 打印进度部分        if count >= 0:            finish_time = time.time()            print count,            print '  ' + str(np.round((finish_time-start_time) - secs_time, 0)) + ' seconds elapsed.'            secs_time = (finish_time-start_time)        count += 1            # 提取所需的universe对应的价格数据    df = df.set_index(['tradeDate','secID'])[price].unstack()    universe = list(set(universe) & set(df.columns))    df.index = pd.to_datetime(df.index, format='%Y-%m-%d')    return df[universe]

def month_ic(factor_data, forward_return_data):    # 计算了每月月末的**因子**和**之后1月收益**的秩相关系数    ic_data = pd.DataFrame(index=factor_data.index, columns=['IC','pValue'])    # 计算相关系数    for dt in ic_data.index:        if dt not in forward_return_data.index:            continue        tmp_factor = factor_data.ix[dt]        tmp_ret = forward_return_data.ix[dt]        fct = pd.DataFrame(tmp_factor)        ret = pd.DataFrame(tmp_ret)        fct.columns = ['fct']        ret.columns = ['ret']        fct['ret'] = ret['ret']        fct = fct[~np.isnan(fct['fct'])][~np.isnan(fct['ret'])]        if len(fct) < 20:            continue        ic, p_value = st.spearmanr(fct['fct'],fct['ret'])   # 计算秩相关系数 RankIC        ic_data['IC'][dt] = ic        ic_data['pValue'][dt] = p_value    ic_data.dropna(inplace=True)        print 'mean of IC: ', ic_data['IC'].mean(), '；',    print 'median of IC: ', ic_data['IC'].median()    print 'the number of IC(all, plus, minus): ', (len(ic_data), len(ic_data[ic_data.IC>0]), len(ic_data[ic_data.IC<0]))    return ic_data

## 获取价格数据price = getUqerPrices('20080101', '20170401', universe, price='openPrice')price[price==0] = np.NaNprice.index = [date.strftime('%Y-%m-%d') for date in price.index]## 计算未来一个月收益率 month_list_1 = []for i in range(len(price)-1):    if price.index[i][0:7] != price.index[i+1][0:7]:        month_list_1.append(price.index[i])month_list_1.append(price.index[-1])month_list_2 = [price.index[0]]for i in range(len(price)-1):    if price.index[i][0:7] != price.index[i+1][0:7]:        month_list_2.append(price.index[i+1])month_list_2end_price = price.ix[month_list_1,:]end_price.index = range(len(end_price))start_price = price.ix[month_list_2,:]start_price.index = range(len(start_price))forward_return_one_month = end_price/start_price-1forward_return_one_month.index = month_list_2

计算因子的IC

OperatingRevenueGrowRate = getUqerStockFactors('20080101', '20170401', universe, 'OperatingRevenueGrowRate')OperatingRevenueGrowRate.index = [date.strftime('%Y-%m-%d') for date in OperatingRevenueGrowRate.index]

OperatingRevenueGrowRate will be calculated for 111 months:

ic_data = month_ic(OperatingRevenueGrowRate, forward_return_one_month)

mean of IC: 0.00617112159861 ；median of IC: 0.000324992135806 the number of IC(all, plus, minus): (111, 56, 55)

BP = 1/getUqerStockFactors('20080101', '20170401', universe, 'PB')BP.index = [date.strftime('%Y-%m-%d') for date in BP.index]

PB will be calculated for 111 months:

ic_data = month_ic(BP, forward_return_one_month)

mean of IC: 0.0393560386847 ；median of IC: 0.0490999880537 the number of IC(all, plus, minus): (111, 68, 43)

NetProfitGrowRate = 1/getUqerStockFactors('20080101', '20170401', universe, 'NetProfitGrowRate')NetProfitGrowRate.index = [date.strftime('%Y-%m-%d') for date in NetProfitGrowRate.index]

NetProfitGrowRate will be calculated for 111 months:

ic_data = month_ic(NetProfitGrowRate, forward_return_one_month)

mean of IC: 0.00433441914357 ；median of IC: 0.00662495246322 the number of IC(all, plus, minus): (111, 60, 51)

data = DataAPI.MktEqudGet(secID=set_universe('A'), beginDate=u"20071201",endDate=u"20170401",isOpen="1", field=u"tradeDate,secID,closePrice",pandas="1")data = data.pivot(index='tradeDate', columns='secID', values='closePrice')RETURNS_1m = data/data.shift(20)-1RETURNS_1m = RETURNS_1m.ix[20:]RETURNS_1m = RETURNS_1m.ix[month_list_2, :]

ic_data = month_ic(returns_1m, forward_return_one_month)

mean of IC: -0.0322389158261 ；median of IC: -0.0400482427638 the number of IC(all, plus, minus): (111, 46, 65)

RETURNS_3m = data/data.shift(60)-1RETURNS_3m = RETURNS_3m.ix[60:]RETURNS_3m = RETURNS_3m.ix[month_list_2, :]

ic_data = month_ic(returns_3m, forward_return_one_month)

mean of IC: -0.0517130560595 ；median of IC: -0.0586121618528 the number of IC(all, plus, minus): (108, 42, 66)

ILLIQUIDITY = 1/getUqerStockFactors('20080101', '20170401', universe, 'ILLIQUIDITY')ILLIQUIDITY.index = [date.strftime('%Y-%m-%d') for date in ILLIQUIDITY.index]

ILLIQUIDITY will be calculated for 111 months:

ic_data = month_ic(ILLIQUIDITY , forward_return_one_month)

mean of IC: -0.129857912846 ；median of IC: -0.142952041084 the number of IC(all, plus, minus): (98, 13, 85)

VOL20= 1/getUqerStockFactors('20080101', '20170401', universe, 'VOL20')VOL20.index = [date.strftime('%Y-%m-%d') for date in VOL20.index]

VOL20 will be calculated for 111 months:

ic_data = month_ic(VOL20 , forward_return_one_month)

mean of IC: 0.0483460315286 ；median of IC: 0.0748837044665 the number of IC(all, plus, minus): (111, 70, 41)

ivr = pd.read_csv('ivr.csv').set_index('Unnamed: 0')ic_data = month_ic(ivr , forward_return_one_month)

mean of IC: -0.0862647515389 ；median of IC: -0.0851817332423 the number of IC(all, plus, minus): (87, 11, 76)

这里我选择了IC的平均值的绝对值大于0.02的因子，因为只是说明问题，我就没有具体去做显著性检验了，检验做起来也比较容易，所以不多说了。而且这里选择的因子比较少，当因子比较多的时候可以适当增加条件。最终我选择了

BP，市净率倒数
RETURNS_1m， 1个月反转收益因子
RETURNS_3m，3个月反转收益因子
ILLIQUIDITY，非流动性因子
VOL20，20日平均换手率因子
IVR，特异度因子

共六个因子。

3 因子筛选

3.1 筛选的流程

假设总共有k个备选的alpha因子F1,F2,…,Fk，我们已经从中筛选出了s个因子Fi1,Fi2,…,Fis（初始时s为0），第s+1次筛选流程如下：

step1 对于剩余备选的alpha因子，每个因子每个月都对Fi1,Fi2,…,Fis做多元回归，计算残差项(s = 0 时不用做这一步)。记得到的K-s个残差项因子分别为θ1,θ2,θk−s。
step2 分别把θj,j=1,2,…,k−s和Fi1,Fi2,…,Fis一起做自变量，做Fama-MacBeth回归，记录θj系数的显著性，和每个月横截面回归R2的平均值。
step3 把系数不显著的因子剔除出备选alpha因子库。
step4 选取系数显著且平均R2最大的因子，假设为θh，则把该因子作为第s+1个筛选出的因子Fis+1，进入第s+2次筛选；
Step5 如果所有因子的系数都不显著，则停止筛选过程。

现在需要对前面六个因子进行筛选。我们首先选择3个月反转收益因子，因为这是我们最先检验是否加入因子库的因子，所以我们只需对其进行Fama—Macbeth检验，如果检验通过，则该因子有效，可以加入因子库。本文对因子的极值处理使用了偏度调整的方法

3.2 步骤的实施

# 预处理returns_3m = RETURNS_3m.iloc[3:]returns_1m = RETURNS_1m.ix[returns_3m.index, :]illiquidity = ILLIQUIDITY.ix[returns_3m.index, :]vol20 = VOL20.ix[returns_3m.index, :]bp = BP.ix[returns_3m.index, :]

# 偏度调整与标准化def adj_boxplot(factor_data):    for i in factor_data.index:        temp = factor_data.ix[i,:]        x = list(temp.dropna())        if len(x) > 0:            mc = sm.stats.stattools.medcouple(x)            x.sort()            q1 = x[int(0.25*len(x))]            q3 = x[int(0.75*len(x))]            iqr = q3-q1            if mc >= 0:                l = q1-1.5*np.exp(-3.5*mc)*iqr                u = q3+1.5*np.exp(4*mc)*iqr            else:                l = q1-1.5*np.exp(-4*mc)*iqr                u = q3+1.5*np.exp(3.5*mc)*iqr            temp[temp < l] = l            temp[temp > u] = u            factor_data.ix[i,:] = (temp-temp.mean())/temp.std()    return factor_datareturns_3m = adj_boxplot(returns_3m)illiquidity = adj_boxplot(illiquidity)returns_1m = adj_boxplot(returns_1m)vol20 = adj_boxplot(vol20)

step1:, 其实第一步就是对3个月反转收益因子进行Fama-Macbeth检验，看看能否加入因子库。

# Fama-Macbeth Regressionlambda_ = []for date in returns_3m.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(forward_return_one_month.ix[date, :].dropna().index))    x = zip(np.array(returns_3m.ix[date, sec_list]))    y = np.array(forward_return_one_month.ix[date, sec_list])        linreg = LinearRegression(fit_intercept=True)      model=linreg.fit(x, y)    lambda_.append(model.coef_[0])

假设检验：

print 'p-value: ', st.ttest_1samp(lambda_, 0)[1]

p-value: 0.00616015864039

p值小于0，所以拒绝原假设，也就是说3个月反转收益因子首先可以加入因子库。这里我们第一次循环就做完了。

**step1:**将BP，RETURNS_1m，ILLIQUIDITY，VOL20，IVR，分别与RETURNS_3m进行回归并得到残差。

theta1 = pd.DataFrame(index=returns_3m.index, columns=returns_3m.columns)for date in returns_3m.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(returns_1m.ix[date, :].dropna().index))    x = zip(np.array(returns_3m.ix[date, sec_list]))    y = np.array(returns_1m.ix[date, sec_list])    if len(x) > 0 and len(y) > 0:        linreg = LinearRegression(fit_intercept=True)          model=linreg.fit(x, y)        y_pred = linreg.predict(x)        theta1.ix[date, sec_list] = y-y_predtheta2 = pd.DataFrame(index=returns_3m.index, columns=returns_3m.columns)for date in returns_3m.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(illiquidity.ix[date, :].dropna().index))    x = zip(np.array(returns_3m.ix[date, sec_list]))    y = np.array(illiquidity.ix[date, sec_list])    if len(x) > 0 and len(y) > 0:        linreg = LinearRegression(fit_intercept=True)          model=linreg.fit(x, y)        y_pred = linreg.predict(x)        theta2.ix[date, sec_list] = y-y_pred theta3 = pd.DataFrame(index=returns_3m.index, columns=returns_3m.columns)for date in returns_3m.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(vol20.ix[date, :].dropna().index))    x = zip(np.array(returns_3m.ix[date, sec_list]))    y = np.array(vol20.ix[date, sec_list])    if len(x) > 0 and len(y) > 0:        linreg = LinearRegression(fit_intercept=True)          model=linreg.fit(x, y)        y_pred = linreg.predict(x)        theta3.ix[date, sec_list] = y-y_pred theta4 = pd.DataFrame(index=returns_3m.index, columns=returns_3m.columns)for date in returns_3m.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(bp.ix[date, :].dropna().index))    x = zip(np.array(returns_3m.ix[date, sec_list]))    y = np.array(bp.ix[date, sec_list])    if len(x) > 0 and len(y) > 0:        linreg = LinearRegression(fit_intercept=True)          model=linreg.fit(x, y)        y_pred = linreg.predict(x)        theta4.ix[date, sec_list] = y-y_pred theta5 = pd.DataFrame(index=ivr.index, columns=ivr.columns)for date in ivr.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(ivr.ix[date, :].dropna().index))    x = zip(np.array(returns_3m.ix[date, sec_list]))    y = np.array(ivr.ix[date, sec_list])    if len(x) > 0 and len(y) > 0:        linreg = LinearRegression(fit_intercept=True)          model=linreg.fit(x, y)        y_pred = linreg.predict(x)        theta5.ix[date, sec_list] = y-y_pred

** step2:**将残差和3个月反转收益因子一起做个Fama-Macbeth回归，记录因子的系数，以及调整的R2

lambd1 = []r_2_1 = []for date in returns_3m.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(forward_return_one_month.ix[date, :].dropna().index)                     & set(theta1.ix[date, :].dropna().index))    if len(sec_list) > 0:        x = np.array([list(returns_3m.ix[date, sec_list]), list(theta1.ix[date, sec_list])]).T        y = np.array(forward_return_one_month.ix[date, sec_list])        linreg = LinearRegression(fit_intercept=True)          model=linreg.fit(x, y)        lambd1.append(model.coef_[1])        r_2_1.append(model.score(x, y))lambd2 = []r_2_2 = []for date in returns_3m.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(forward_return_one_month.ix[date, :].dropna().index)                     & set(theta2.ix[date, :].dropna().index))    if len(sec_list) > 0:        x = np.array([list(returns_3m.ix[date, sec_list]), list(theta2.ix[date, sec_list])]).T        y = np.array(forward_return_one_month.ix[date, sec_list])        linreg = LinearRegression(fit_intercept=True)          model=linreg.fit(x, y)        lambd2.append(model.coef_[1])        r_2_2.append(model.score(x, y))    lambd3 = []r_2_3 = []for date in returns_3m.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(forward_return_one_month.ix[date, :].dropna().index)                     & set(theta3.ix[date, :].dropna().index))    if len(sec_list) > 0:        x = np.array([list(returns_3m.ix[date, sec_list]), list(theta3.ix[date, sec_list])]).T        y = np.array(forward_return_one_month.ix[date, sec_list])        linreg = LinearRegression(fit_intercept=True)          model=linreg.fit(x, y)        lambd3.append(model.coef_[1])        r_2_3.append(model.score(x, y))        lambd4 = []r_2_4 = []for date in returns_3m.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(forward_return_one_month.ix[date, :].dropna().index)                     & set(theta4.ix[date, :].dropna().index))    if len(sec_list) > 0:        x = np.array([list(returns_3m.ix[date, sec_list]), list(theta4.ix[date, sec_list])]).T        y = np.array(forward_return_one_month.ix[date, sec_list])        linreg = LinearRegression(fit_intercept=True)          model=linreg.fit(x, y)        lambd4.append(model.coef_[1])        r_2_4.append(model.score(x, y))        lambd5 = []r_2_5 = []for date in ivr.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(forward_return_one_month.ix[date, :].dropna().index)                     & set(theta5.ix[date, :].dropna().index))    if len(sec_list) > 0:        x = np.array([list(returns_3m.ix[date, sec_list]), list(theta5.ix[date, sec_list])]).T        y = np.array(forward_return_one_month.ix[date, sec_list])        linreg = LinearRegression(fit_intercept=True)          model=linreg.fit(x, y)        lambd5.append(model.coef_[1])        r_2_5.append(model.score(x, y))

step3，step4: 再来看看系数的显著性,剔除那些不显著的因子，选择显著性检验通过并且横截面回归R2平均值最大的因子。

print u'1个月反转收益因子' , 'p-value: ', st.ttest_1samp(lambd1, 0)[1],';', '可决系数均值：', np.mean(r_2_1)print u'非流动性因子' , 'p-value: ',st.ttest_1samp(lambd2, 0)[1], ';', '可决系数均值：', np.mean(r_2_2)print u'20日换手率因子' , 'p-value: ',st.ttest_1samp(lambd3, 0)[1], ';', '可决系数均值：', np.mean(r_2_3)print u'BP因子' , 'p-value: ',st.ttest_1samp(lambd4, 0)[1], ';', '可决系数均值：', np.mean(r_2_4)print u'IVR因子' , 'p-value: ',st.ttest_1samp(lambd5, 0)[1], ';', '可决系数均值：', np.mean(r_2_5)

1个月反转收益因子 p-value: 0.941194888256 ; 可决系数均值：0.0311845405958 非流动性因子 p-value: 6.49532628633e-05 ; 可决系数均值：0.033727514696 20日换手率因子 p-value: 0.948573256553 ; 可决系数均值：0.02703786586 BP因子 p-value: 0.92448984796 ; 可决系数均值：0.0388933569553 IVR因子 p-value: 3.14949437888e-10 ; 可决系数均值：0.0253165524167

这样我们第一步应该保留非流动性因子,而1个月反转收益因子，20日换手率因子，BP因子因为系数不显著，予以剔除。

现在应该进入第三次筛选，考察是否加入特异度因子。

theta = pd.DataFrame(index=ivr.index, columns=ivr.columns)for date in ivr.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(ivr.ix[date, :].dropna().index) & set(illiquidity.ix[date, :].dropna().index))    x = np.array([list(returns_3m.ix[date, sec_list]), list(illiquidity.ix[date, sec_list])]).T    y = np.array(ivr.ix[date, sec_list])    if len(x) > 0 and len(y) > 0:        linreg = LinearRegression(fit_intercept=True)          model=linreg.fit(x, y)        y_pred = linreg.predict(x)        theta.ix[date, sec_list] = y-y_pred

lambd = []r_2 = []for date in ivr.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(forward_return_one_month.ix[date, :].dropna().index)                     & set(theta.ix[date, :].dropna().index) & set(illiquidity.ix[date, :].dropna().index))    if len(sec_list) > 0:        x = np.array([list(returns_3m.ix[date, sec_list]), list(illiquidity.ix[date, sec_list]), list(theta.ix[date, sec_list])]).T        y = np.array(forward_return_one_month.ix[date, sec_list])        linreg = LinearRegression(fit_intercept=True)          model=linreg.fit(x, y)        lambd.append(model.coef_[2])        r_2.append(model.score(x, y))

print u'IVR因子' , 'p-value: ',st.ttest_1samp(lambd, 0)[1], ';', '可决系数均值：', np.mean(r_2)

IVR因子 p-value: 4.2880711008e-10 ; 可决系数均值：0.0411817522236

IVR因子系数的显著性检验通过，所以应该把IVR因子加入到因子库当中。

3.3 可决系数的变化

我们最终选择了三个因子，分别是3个月反转收益因子，非流动性因子，还有特异度因子，我们看看在筛选过程中横截面回顾可决系数的变化。

# Fama-Macbeth Regressionr_2_mean = []r_2 = []for date in ivr.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(forward_return_one_month.ix[date, :].dropna().index))    x = zip(np.array(returns_3m.ix[date, sec_list]))    y = np.array(forward_return_one_month.ix[date, sec_list])        linreg = LinearRegression(fit_intercept=True)      model=linreg.fit(x, y)    r_2.append(model.score(x, y))r_2_mean.append(np.mean(r_2))r_2 = []for date in ivr.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(forward_return_one_month.ix[date, :].dropna().index)                   & set(illiquidity.ix[date, :].dropna().index))    x = np.array([list(returns_3m.ix[date, sec_list]), list(illiquidity.ix[date, sec_list])]).T    y = np.array(forward_return_one_month.ix[date, sec_list])        linreg = LinearRegression(fit_intercept=True)      model=linreg.fit(x, y)    r_2.append(model.score(x, y))r_2_mean.append(np.mean(r_2))r_2 = []for date in ivr.index:    sec_list = list(set(returns_3m.ix[date, :].dropna().index) & set(forward_return_one_month.ix[date, :].dropna().index)                   & set(illiquidity.ix[date, :].dropna().index) & set(ivr.ix[date, :].dropna().index))    x = np.array([list(returns_3m.ix[date, sec_list]), list(illiquidity.ix[date, sec_list]), list(ivr.ix[date, sec_list])]).T    y = np.array(forward_return_one_month.ix[date, sec_list])        linreg = LinearRegression(fit_intercept=True)      model=linreg.fit(x, y)    r_2.append(model.score(x, y))r_2_mean.append(np.mean(r_2))

# r_2_mean = pd.DataFrame(data=r_2_mean, index=['return_1_m', 'illiquidity', 'ivr'])fig = plt.figure(figsize=(8, 6))ax = fig.add_subplot(111)ax = r_2_mean.plot(kind='bar', ax=ax, legend=False)s = ax.set_title('$R^{2}$')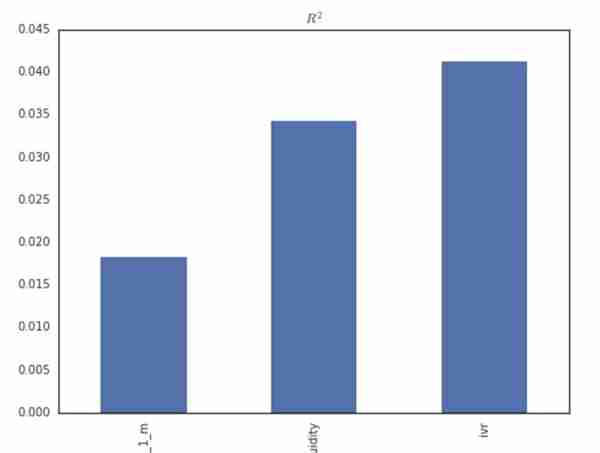

虽然因子数量比较少，但是从上图也可以看出，再添加第二个因子后，R2有了一定程度的提高，但添加了特异度因子后，提高的幅度有所减小，说明新因子给因子库增加的信息有限。